Multi-Armed Bandit Problem
The multi-armed bandit problem is a classic example in reinforcement learning and decision theory. It is framed around the idea of a gambler facing multiple slot machines (bandits), each with an unknown probability of payout. The gambler must decide which machine to play in order to maximize the total reward over time. This involves a trade-off between exploration (trying different machines to discover their payout rates) and exploitation (playing the machine that has the highest known payout rate).
Problem Setup:
- We have three slot machines
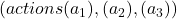 .
. - The true expected rewards (which are unknown to us initially) are:
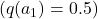
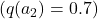
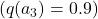
Initial Action-Value Estimates
Let’s consider two cases:
Case 1: Realistic Initial Values
We set the initial action-value estimates to 0:
Case 2: Optimistic Initial Values
We set optimistic initial action-value estimates:
Step 1: Action Selection and Learning
Realistic Initial Values
- In the first step, since all actions have the same initial value
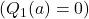 , the algorithm randomly chooses one action. Let’s say it chooses
, the algorithm randomly chooses one action. Let’s say it chooses 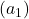 .
. - The true expected reward for
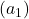 is
is 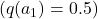 , but the actual observed reward
, but the actual observed reward 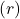 may vary around this true mean due to randomness. Suppose you observe
may vary around this true mean due to randomness. Suppose you observe 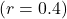 .
. - The estimate is updated using:
![Rendered by QuickLaTeX.com [Q_2(a_1) = Q_1(a_1) + \alpha \cdot (r - Q_1(a_1))]](https://orionsunrise.com/wp-content/ql-cache/quicklatex.com-d91508a89acc8be8f873be1771f91262_l3.png)
Assuming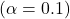 (a small learning rate):
(a small learning rate):![Rendered by QuickLaTeX.com [Q_2(a_1) = 0 + 0.1 \times (0.4 - 0) = 0.04]](https://orionsunrise.com/wp-content/ql-cache/quicklatex.com-fe893d6ca1316a0dd714f39a34e631ef_l3.png)
- Now,
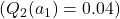 , while
, while 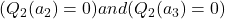 . The algorithm might still pick
. The algorithm might still pick 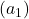 because it has the highest estimate so far, leading to more exploitation of
because it has the highest estimate so far, leading to more exploitation of 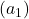 and less exploration of other actions.
and less exploration of other actions.
Optimistic Initial Values
- Initially, all actions have an estimated value of
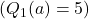 . The algorithm randomly picks one action
. The algorithm randomly picks one action 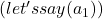 .
. - The true expected reward for
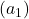 is
is 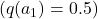 , and you observe a reward
, and you observe a reward 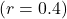 (as before).
(as before). - The estimate is updated:
![Rendered by QuickLaTeX.com [Q_2(a_1) = 5 + 0.1 \times (0.4 - 5) = 5 - 0.46 = 4.54]](https://orionsunrise.com/wp-content/ql-cache/quicklatex.com-a036cded6ec4073bd6046283975f288d_l3.png)
- Now,
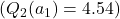 , but
, but 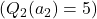 and
and 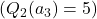 . The algorithm is likely to pick
. The algorithm is likely to pick 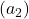 or
or 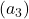 next because they still have higher estimates, leading to exploration.
next because they still have higher estimates, leading to exploration.
Step 2: Convergence Over Time
- Realistic Initial Values: The algorithm may get stuck in a suboptimal action because the initial estimates do not encourage exploration.
- Optimistic Initial Values: The algorithm quickly explores other actions because the high initial estimates lead to “disappointment” when actual rewards are lower, driving the algorithm to try other options.
Summary:
- With realistic initial values, the algorithm’s learning is driven more by the rewards observed, potentially leading to slower exploration.
- With optimistic initial values, the algorithm is pushed to explore more actions early on, which can lead to quicker discovery of the best action.
Multi-Armed Bandit Problem
Optimistic Initial Values
The section discusses how the initial estimates of the action values ![]() (the expected rewards for taking action
(the expected rewards for taking action ![]() ) can influence the performance of the learning algorithm.
) can influence the performance of the learning algorithm.
- Initial Action-Value Estimates:
- In many learning methods, the initial estimates of action values
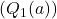 are crucial. If these estimates are set too high or too low, they can bias the learning process.
are crucial. If these estimates are set too high or too low, they can bias the learning process. - For example, if you set
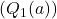 to a high value (optimistic initial values), it encourages the algorithm to explore different actions more thoroughly because the algorithm initially expects high rewards from all actions. This exploration can help the algorithm discover the true action values more quickly.
to a high value (optimistic initial values), it encourages the algorithm to explore different actions more thoroughly because the algorithm initially expects high rewards from all actions. This exploration can help the algorithm discover the true action values more quickly.
- Bias and Exploration:
- It is mentioned that methods with constant step-size parameters
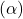 (as in some forms of learning algorithms) retain this bias throughout learning because they do not fully converge to the true action values.
(as in some forms of learning algorithms) retain this bias throughout learning because they do not fully converge to the true action values. - The optimistic initial values essentially act as a built-in mechanism to encourage exploration. If the initial action values are optimistic (e.g.,
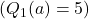 ), the learner will initially be “disappointed” with the rewards it receives since they are likely lower than expected. This disappointment leads the algorithm to try other actions.
), the learner will initially be “disappointed” with the rewards it receives since they are likely lower than expected. This disappointment leads the algorithm to try other actions.
- Greedy vs. ( \varepsilon )-Greedy Methods:
- The section compares the performance of a greedy method with optimistic initial values
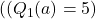 ,
, 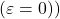 to a more realistic
to a more realistic 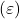 -greedy method
-greedy method 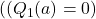 ,
, 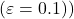 . The greedy method with optimistic values starts by exploring more due to its initial high expectations but eventually settles into exploitation. The
. The greedy method with optimistic values starts by exploring more due to its initial high expectations but eventually settles into exploitation. The 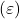 -greedy method balances exploration and exploitation more evenly but might not perform as well initially due to the lack of an optimistic bias.
-greedy method balances exploration and exploitation more evenly but might not perform as well initially due to the lack of an optimistic bias.
- Practical Implications:
- The technique of setting optimistic initial values is simple but effective, especially in stationary problems (where the reward probabilities don’t change over time). However, it is less effective in nonstationary problems (where the reward probabilities can change) because the exploration it encourages is temporary.

- The figure illustrates the effect of optimistic initial values on the performance of a learning algorithm in a 10-armed bandit problem. The black line shows the performance of a greedy method with optimistic initial values
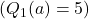 , while the gray line shows the performance of an
, while the gray line shows the performance of an 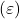 -greedy method with more realistic initial values
-greedy method with more realistic initial values 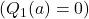 .
. - The optimistic method performs better initially due to increased exploration but eventually performs similarly to the
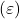 -greedy method as the initial bias diminishes over time.
-greedy method as the initial bias diminishes over time.
Conclusion
Optimistic initial values are a simple yet effective way to encourage exploration in reinforcement learning algorithms. By setting higher-than-realistic initial values for expected rewards, the algorithm is nudged into exploring different actions before settling into exploiting the best-known action. This approach is particularly useful in stationary environments but may not be as beneficial in nonstationary environments where exploration needs to be ongoing.