Part 1: Action-Value Methods
The term “action-value method” refers to a set of techniques used in reinforcement learning to estimate the expected reward (or value) associated with taking a particular action in a given environment. These methods are central to decision-making processes in reinforcement learning, where an agent aims to maximize its cumulative reward by selecting actions based on these estimated values.
Key Concepts:
- Action-Value (Q-Value):
- The action value of an action a, denoted as Q(a), represents the expected reward an agent can expect to receive if it chooses action a.
- Formally, Q(a) is defined as the expected sum of rewards received after taking action a, assuming the agent follows a particular strategy (policy) thereafter.
- Estimating Action Values:
- Since the true action values are typically unknown, the agent needs to estimate them based on its interactions with the environment.
- The estimation is done by updating the action values iteratively as the agent experiences the outcomes (rewards) of its actions.
- Exploration vs. Exploitation:
- A core challenge in reinforcement learning is balancing exploration (trying out different actions to discover their values) and exploitation (choosing actions that are currently believed to have the highest value).
- Action-value methods help navigate this trade-off by guiding the agent’s decisions based on the estimated values of actions.
- Importance of Action-Value Methods:
- Guiding Decision-Making:
- Action-value methods provide the agent with a way to make informed decisions by estimating the potential outcomes of different actions.
- Learning from Experience:
- These methods allow the agent to improve its strategy over time by continuously refining its estimates based on new experiences.
- Adaptability:
- Action-value methods can be adapted to both stationary and nonstationary environments, enabling the agent to handle a wide range of real-world scenarios.
- Guiding Decision-Making:
What is an Action-Value Method?
An action-value method is a way to estimate the value of taking a particular action in a given situation based on the rewards that action has provided in the past. The value of an action is typically defined as the average of the rewards received when that action was taken.
Simple Example: Choosing a Vending Machine
Imagine you are at a location with two vending machines, Machine A and Machine B, and you want to figure out which machine is more likely to give you a good snack. You only have a limited number of coins, so you need to make smart choices to maximize your satisfaction (reward) from the snacks you receive.
How the Action-Value Method Works:
- Actions: In this example, your actions are choosing between Machine A and Machine B.
- Rewards: Each time you choose a machine, you get a reward based on how much you like the snack. The reward could be, for example, a score from 1 to 10, where 10 means you loved the snack and 1 means you didn’t like it.
- Estimating Action Values:
- You start without knowing which machine is better, so you try each one.
- Let’s say the first time you use Machine A, you get a snack you rate as 7 out of 10. For Machine B, you rate the snack as 5 out of 10. After trying each machine once, your initial action-value estimates might be:
- ( Q(A) = 7 ) (after 1 use)
- ( Q(B) = 5 ) (after 1 use)
- Updating Action Values:
- You keep trying the machines and updating the estimates based on the rewards you receive.
- Suppose the next time you use Machine A, you get a snack you rate as 8 out of 10. Now you update the action value for Machine A. The action-value method might update the estimate as the average of the rewards you’ve received so far:
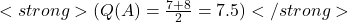 (after 2 uses)
(after 2 uses)- Machine B’s value remains
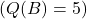 because you haven’t tried it again yet.
because you haven’t tried it again yet.
- Using the Estimates:
- After several trials, you might find:
- ( Q(A) = 7.5 )
- ( Q(B) = 6 )
- You can now use these estimates to guide your future decisions, favoring Machine A because it has a higher estimated value.
Summary of Action-Value Method:
- Action-Value Method: A way to estimate how good it is to take a certain action (like choosing a vending machine) based on the average rewards you’ve received from that action in the past.
- Purpose: Helps you make decisions that maximize your long-term rewards by identifying the actions that have historically given the best outcomes.
- Learning: Over time, as you gather more data (rewards) from each action, your estimates become more accurate, helping you make better choices.
In essence, the action-value method is about learning from experience to make better decisions in the future. It’s a core concept in reinforcement learning, where agents use such methods to maximize their cumulative rewards over time.
Action-Value Methods
- Objective:
- This section introduces simple methods for estimating the values of actions and using these estimates to make action selection decisions.
- Notation:
- The true (actual) value of an action
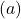 is denoted as
is denoted as 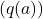 .
. - The estimated value of an action at time step
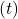 is denoted as
is denoted as 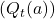 .
.
- The true (actual) value of an action
- Estimating Action Values:
- The true value of an action is the mean reward received when that action is selected.
- A natural way to estimate this value is by averaging the rewards received each time the action is selected.
- Mathematically, if an action ( a ) has been chosen
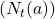 times before time step ( t ), yielding rewards
times before time step ( t ), yielding rewards  , the estimated value is given by:
, the estimated value is given by: 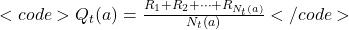
- If
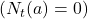 , a default value is used for
, a default value is used for 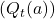 , typically
, typically 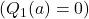 .
. - As
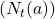 increases (approaches infinity), by the law of large numbers,
increases (approaches infinity), by the law of large numbers, 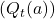 converges to
converges to 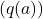 .
. - This method is referred to as the sample-average method because it averages a sample of the relevant rewards to estimate action values.
Part 2: Greedy Action Selection
- Simplest Selection Rule:
- The simplest rule for selecting actions is to choose the action (or one of the actions) with the highest estimated value at step ( t ). This is known as greedy action selection.
- Mathematically, this can be expressed as:
- Here,
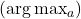 denotes the action
denotes the action 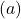 for which
for which 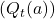 is maximized. Ties are broken arbitrarily.
is maximized. Ties are broken arbitrarily.
- Exploitation:
- Greedy action selection focuses on exploiting current knowledge to maximize immediate reward.
- It does not spend time sampling actions with lower estimated values, which might potentially be better upon further exploration.
- ε-Greedy Methods:
- A variation on greedy action selection is the ε-greedy method:
- Greedy Most of the Time: Most of the time, the action with the highest estimated value is selected (as in the greedy method).
- Exploration Occasionally: With a small probability
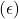 , a random action is selected, allowing exploration.
, a random action is selected, allowing exploration. - This approach ensures that every action is sampled an infinite number of times as the number of plays increases, guaranteeing that
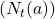 increases for all
increases for all 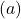 and that
and that 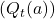 converges to
converges to 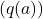 .
.
- Asymptotic Guarantees:
- The ε-greedy method guarantees that the probability of selecting the optimal action converges to
 (i.e., very close to certainty).
(i.e., very close to certainty). - However, these are asymptotic guarantees and may not reflect practical effectiveness in the short term.
- The ε-greedy method guarantees that the probability of selecting the optimal action converges to
Part 3: Assessing Greedy vs. ε-Greedy Methods
- Comparative Evaluation:
- To assess the effectiveness of greedy and ε-greedy methods, the text describes a numerical comparison conducted on a set of test problems known as the 10-armed testbed.
- Test Setup:
- The test involved 2000 randomly generated n-armed bandit tasks with
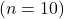 .
. - The true action values
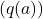 for each action
for each action 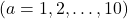 were selected from a normal (Gaussian) distribution with a mean of 0 and variance of 1.
were selected from a normal (Gaussian) distribution with a mean of 0 and variance of 1. - For a given bandit task, the actual reward
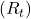 at time step
at time step 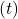 was the true action value
was the true action value 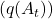 plus a normally distributed noise term with mean 0 and variance 1.
plus a normally distributed noise term with mean 0 and variance 1.
- The test involved 2000 randomly generated n-armed bandit tasks with
- Performance Measures:
- The methods were evaluated based on their average performance over 2000 tasks.
- Two key performance measures were used:
- Average reward: The reward averaged over all time steps.
- % Optimal action: The percentage of time steps on which the optimal action was selected.
- Results Overview:

- Graphs Explanation:
- The upper graph shows the average reward over time for a greedy method and two ε-greedy methods
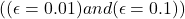 .
. - The lower graph shows the percentage of time steps during which the optimal action was selected.
- The upper graph shows the average reward over time for a greedy method and two ε-greedy methods
- Greedy Method Performance:
- The greedy method initially improved faster than the ε-greedy methods but quickly leveled off at a lower reward level.
- It achieved a reward per step of around 1, whereas the best possible reward on this testbed was about 1.55.
- The greedy method performed significantly worse in the long run because it often got stuck performing suboptimal actions.
- The lower graph shows that the greedy method found the optimal action in only about one-third of the tasks, and it never returned to it in the other two-thirds.
- ε-Greedy Method Performance:
- The ε-greedy methods performed better in the long run because they continued to explore and improve their chances of recognizing the optimal action.
- The
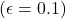 method explored more, finding the optimal action earlier, but never selected it more than 91% of the time.
method explored more, finding the optimal action earlier, but never selected it more than 91% of the time. - The
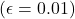 method improved more slowly but eventually performed better than the
method improved more slowly but eventually performed better than the 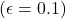 method on both performance measures.
method on both performance measures. - It’s possible to reduce
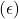 over time to get the best of both high and low values.
over time to get the best of both high and low values.
Part 4: Advantages and Challenges of ε-Greedy Methods
- Task Dependency:
- The advantage of ε-greedy over greedy methods depends on the task at hand.
- For example, if the reward variance is large (e.g., 10 instead of 1), more exploration is required to find the optimal action.
- In this case, ε-greedy methods are likely to perform better relative to the greedy method.
- If the reward variances were zero, the greedy method might perform best because it would find the optimal action and stick with it, never exploring again.
- Exploration in Nonstationary Environments:
- In nonstationary environments, where the true values of actions change over time, exploration is crucial even for the deterministic case.
- This is because the non-greedy actions might change and become better than the greedy one.
- In reinforcement learning, nonstationarity is often encountered, requiring a balance between exploration and exploitation.
- Effective Nonstationarity:
- Even if the underlying task is stationary and deterministic, the learner faces a set of bandit-like decision tasks, each of which changes over time due to the learning process itself.
- This makes effective nonstationarity a common scenario in reinforcement learning, highlighting the need for balancing exploration and exploitation.
Summary:
- Part 3 discusses the numerical comparison between greedy and ε-greedy methods, demonstrating that while greedy methods may perform well initially, they often get stuck with suboptimal actions in the long run. ε-greedy methods, by continuing to explore, improve their performance over time.
- Part 4 explains that the advantages of ε-greedy methods depend on the nature of the task and emphasizes the importance of exploration in nonstationary environments, which is a typical challenge in reinforcement learning.
To build intuition behind the concept of estimating action values using the sample-average method, let’s break down the idea into a more intuitive understanding, using a real-world analogy.
Real-World Analogy: Slot Machine Example
Imagine you’re in a casino with several slot machines, each with its own payout rate. However, you don’t know these rates in advance. Your goal is to maximize your winnings by playing these machines. Here’s how the intuition behind estimating action values works:
- Unknown Payout Rates (True Value,
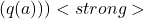 :
:
- Each slot machine has a true payout rate—say 10% on one machine, 15% on another, etc. This payout rate is the machine’s true value
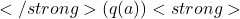 . But, like any gambler, you don’t know this value ahead of time.
. But, like any gambler, you don’t know this value ahead of time.
- Estimating Payout Rates (Estimated Value,
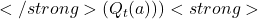 :
:
- Every time you play a machine (take an action), you observe whether you win or lose (receive a reward). Over time, as you play a machine more and more, you start forming an estimate of its payout rate based on your observed wins and losses.
- After playing a machine several times, you calculate the average payout you’ve received from that machine. This average is your best guess of the machine’s true payout rate. This is what
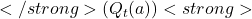 represents—the average reward you’ve observed up to time step
represents—the average reward you’ve observed up to time step 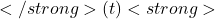 .
.
- Building Confidence:
- Initially, your estimate might be off because you’ve only played the machine a few times. But as you keep playing (i.e., as
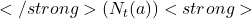 increases), your estimate becomes more accurate. The more times you play, the closer your average payout (estimated value,
increases), your estimate becomes more accurate. The more times you play, the closer your average payout (estimated value, 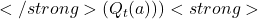 will get to the machine’s true payout rate
will get to the machine’s true payout rate 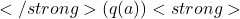 .
.
- Why Averaging Works:
- The reason averaging works well is rooted in the law of large numbers. This law tells us that as the number of trials increases, the sample average (what you observe) converges to the expected value (the true underlying rate).
- So, if you keep playing the same slot machine, your observed average payout will converge to its true payout rate.
- Practical Decision-Making:
- In practice, after you’ve formed an estimate
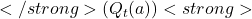 for each machine (action), you can use this information to decide which machine to play next. Typically, you’d want to play the machine with the highest estimated payout rate, but sometimes, to ensure your estimates are accurate, you might choose to test other machines occasionally (exploration).
for each machine (action), you can use this information to decide which machine to play next. Typically, you’d want to play the machine with the highest estimated payout rate, but sometimes, to ensure your estimates are accurate, you might choose to test other machines occasionally (exploration).
Intuition Summary
- Estimated Value
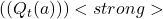 : It’s like your current best guess of how good a slot machine is, based on the average of what you’ve seen so far.
: It’s like your current best guess of how good a slot machine is, based on the average of what you’ve seen so far. - True Value
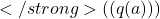 : The actual long-term average payout rate of the machine, which you’re trying to discover.
: The actual long-term average payout rate of the machine, which you’re trying to discover. - Sample-Average Method: This is simply taking the average of your observations to get a better and better guess of the true value as you gather more data.
Visualization:
- Early Stages: When you’ve only pulled the lever a few times, your estimate
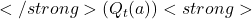 might fluctuate a lot because of limited data.
might fluctuate a lot because of limited data. - Later Stages: As you play more, the fluctuations decrease, and
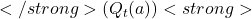 stabilizes closer to
stabilizes closer to 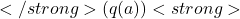 .
.
The key takeaway is that the sample-average method is a natural, straightforward approach that works well when you want to estimate something that you observe repeatedly. The more you observe, the more confident you become in your estimate, which helps you make better decisions in the long run.
1. Greedy Action Selection
- Objective:
- The goal is to decide which action to take at each time step to maximize rewards. The greedy action selection rule is the simplest approach to this decision-making process.
- The Greedy Rule:
- At each time step
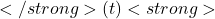 , the action
, the action 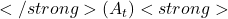 selected is the one with the highest estimated value ( Q_t(a) ).
selected is the one with the highest estimated value ( Q_t(a) ). - Mathematically, this is expressed as:
-
- Here,
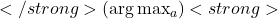 denotes the action
denotes the action 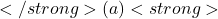 for which the estimated value
for which the estimated value 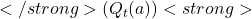 is maximized. If there is a tie (multiple actions have the same estimated value), the tie is broken arbitrarily.
is maximized. If there is a tie (multiple actions have the same estimated value), the tie is broken arbitrarily. - Intuition Behind the Greedy Rule:
- Exploitation: Greedy action selection is all about exploitation—making the best use of the current knowledge. Since the action with the highest estimated value is chosen, this method aims to maximize immediate reward.
- No Exploration: The greedy rule doesn’t spend any time exploring actions that have lower estimated values, even if those actions might turn out to be better in the long run after further exploration.
2. Introducing ( \epsilon ) -Greedy Methods
- Limitation of Pure Greedy Strategy:
- While the greedy strategy is straightforward, it has a major drawback: it might miss out on actions that could yield higher rewards in the long term because it never explores them. This can cause the strategy to get stuck in a local optimum, where it consistently selects a suboptimal action.
- The ( \epsilon ) -Greedy Strategy:
- To address the limitation of the pure greedy strategy, the
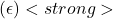 -greedy method is introduced:
-greedy method is introduced:
- Greedy Most of the Time: The action with the highest estimated value is selected most of the time (with probability ( 1 – \epsilon )).
- Random Exploration Occasionally: With a small probability ( \epsilon ), a random action is selected. This random selection allows for exploration of other actions that might have been overlooked by the greedy strategy.
- This approach ensures that every action has some chance of being selected, which helps in discovering the actual best action over time.
- Benefits of ( \epsilon ) -Greedy Strategy:
- As the number of plays increases, every action will eventually be sampled an infinite number of times. This ensures that:
- The count
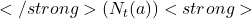 for each action
for each action 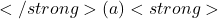 goes to infinity.
goes to infinity. - The estimated value
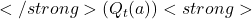 will converge to the true value
will converge to the true value 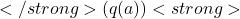 .
.
- The count
- Optimal Action Selection:
- The probability of selecting the optimal action converges to ( 1 – \epsilon ), which is close to certainty if ( \epsilon ) is small. This means that over time, the ( \epsilon ) -greedy method becomes increasingly likely to choose the best possible action.
3. Asymptotic Guarantees vs. Practical Effectiveness
- Asymptotic Guarantees:
- The theory provides asymptotic guarantees: as the number of trials goes to infinity, the ( \epsilon )-greedy method will almost surely converge on the best action.
- Practical Considerations:
- However, these guarantees only apply in the long run. In practical scenarios, where the number of trials might be limited, the actual performance might differ.
- The ( \epsilon )-greedy method might still perform suboptimally in finite time, especially if ( \epsilon ) is not chosen carefully or if the exploration phase results in frequent random choices.
Summary of Key Concepts
- Greedy Action Selection focuses purely on exploiting the current best estimate of action values, aiming for immediate rewards without considering the potential of unexplored actions.
- ( \epsilon ) -Greedy Methods introduce a balance between exploration and exploitation. By occasionally selecting actions randomly, this method prevents the algorithm from getting stuck in suboptimal choices and helps it discover better actions over time.
- Asymptotic Behavior: While the ( \epsilon )-greedy method has strong theoretical guarantees in the long run, its practical effectiveness depends on the specific problem and the choice of ( \epsilon ) .
Understanding these methods provides a foundation for more complex decision-making strategies in reinforcement learning, where balancing exploration and exploitation is a central challenge.
To develop an intuitive understanding of the greedy and ( \epsilon ) -greedy action selection methods, let’s use a real-world analogy involving everyday decision-making.
Intuition Behind Greedy Action Selection
Scenario:
Imagine you’ve just moved to a new city and are exploring different restaurants for lunch. Over a few days, you’ve tried several places and found one that consistently serves great food (say, a sushi place). Based on your experience, this sushi place has become your favorite, and you believe it’s the best option.
Greedy Strategy:
- Exploitation: Every day, you decide to go to this sushi place because you know from experience that it offers great food. This decision is based purely on maximizing your immediate satisfaction—you’re exploiting the knowledge you have.
- No Exploration: You stop trying other restaurants because you think you’ve already found the best one. But what if there’s an even better restaurant nearby that you never tried? By sticking to your favorite, you might miss out on discovering an even better option.
Drawback:
- The problem with the greedy strategy is that you might get stuck with a good, but not the best, choice. If there’s a hidden gem of a restaurant just a block away, you’d never know because you’ve stopped exploring.
Intuition Behind ( \epsilon ) -Greedy Methods
Scenario Continued:
Now, let’s tweak your strategy a bit. Instead of always going to the sushi place, you decide to mix things up.
( \epsilon ) -Greedy Strategy:
- Mostly Greedy: Most of the time (say, 90% of the time), you still go to the sushi place because it’s your favorite and you know it’s good.
- Occasional Exploration: But occasionally (say, 10% of the time), you decide to try a new restaurant randomly. Maybe you pick a place that looks interesting or one that you’ve heard good things about but haven’t tried yet.
Benefits:
- Discovering New Favorites: By occasionally trying new places, you give yourself a chance to discover a restaurant that’s even better than your current favorite. If you find a better one, your “favorite” might change, and you’ll start going there more often.
- Avoiding Local Optima: This strategy prevents you from getting stuck with a suboptimal choice just because you never explored enough. Even if the sushi place is good, maybe there’s a fantastic Italian place that’s even better.
The Long Run:
- Over time, this strategy ensures that you’ve tried all the available options multiple times. Eventually, you’ll be able to identify the absolute best restaurant in the area and enjoy it frequently, but without completely giving up on the possibility of finding something even better.
Summary of Intuitive Insights
- Greedy Strategy:
- Like always going to your favorite restaurant because you believe it’s the best based on your experience so far. It’s simple and focuses on maximizing immediate benefits but might miss out on better options.
- ( \epsilon ) -Greedy Strategy:
- Like going to your favorite restaurant most of the time but occasionally trying something new just in case there’s a better option out there. It balances the need for immediate satisfaction with the possibility of discovering even better choices over time.
This balance between exploitation (enjoying what you know is good) and exploration (trying new things to see if there’s something better) is at the heart of the ( \epsilon )-greedy method. It ensures that you don’t get stuck with a merely “good” choice when there could be something “great” that you haven’t discovered yet.
Intuitive Explanation with Maths
Sure! Let’s build an intuitive example involving math, where we’ll apply the greedy and ( \epsilon )-greedy strategies and break down the formulas involved.
Example: Choosing the Best Slot Machine
Scenario:
You’re at a casino with three different slot machines (let’s call them A, B, and C). Each machine has a different probability of paying out, but you don’t know these probabilities in advance. Your goal is to maximize your winnings over time by choosing which machine to play.
- True Probabilities:
- Machine A: 40% chance of winning (probability ( q(A) = 0.4 ))
- Machine B: 50% chance of winning (probability ( q(B) = 0.5 ))
- Machine C: 60% chance of winning (probability ( q(C) = 0.6 ))
You don’t know these probabilities initially, so you have to estimate them based on your experience.
Step 1: Estimating Action Values (Sample-Average Method)
Every time you play a machine, you record whether you win or lose. Over time, you calculate the average payout for each machine, which becomes your estimate of that machine’s probability of winning.
- Estimated Value
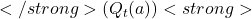 :
: - If you’ve played machine
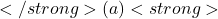 (say, Machine A)
(say, Machine A) 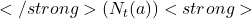 times by time step ( t ) and won
times by time step ( t ) and won  times (where each
times (where each 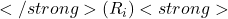 is 1 if you win and 0 if you lose), the estimated value
is 1 if you win and 0 if you lose), the estimated value 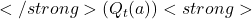 is given by:
is given by: ![Rendered by QuickLaTeX.com </strong> [Q_t(a) = \frac{R_1 + R_2 + \dots + R_{N_t(a)}}{N_t(a)}] <strong>](https://orionsunrise.com/wp-content/ql-cache/quicklatex.com-7d3935482a3e68d6bfe520346778118c_l3.png)
- LaTeX:
Q_t(a) = \frac{R_1 + R_2 + \dots + R_{N_t(a)}}{N_t(a)}
- LaTeX:
- This is the sample average of your wins. For example, if you played Machine A 5 times and won 2 times, the estimated value ( Q_t(A) ) would be: [
Q_t(A) = \frac{1 + 0 + 1 + 0 + 0}{5} = \frac{2}{5} = 0.4
] - After many plays, this estimate ( Q_t(a) ) should get closer to the true value ( q(a) ) (the actual probability of winning on that machine).
Step 2: Greedy Action Selection
Now, let’s apply the greedy strategy:
- Greedy Rule:
- At each time step ( t ), you choose the machine ( a ) with the highest estimated value ( Q_t(a) ): [
A_t = \arg\max_a Q_t(a)
]- LaTeX:
A_t = \arg\max_a Q_t(a)
- LaTeX:
- Suppose after a few rounds, you have the following estimates:
- ( Q_t(A) = 0.3 )
- ( Q_t(B) = 0.4 )
- ( Q_t(C) = 0.5 )
- The greedy strategy would then choose Machine C, as it has the highest estimated probability of winning (0.5).
Step 3: ( \epsilon )-Greedy Action Selection
Now, let’s consider the ( \epsilon )-greedy strategy:
- ( \epsilon )-Greedy Rule:
- Most of the time (with probability ( 1 – \epsilon )), you choose the machine with the highest estimated value ( Q_t(a) ) (as in the greedy strategy).
- Occasionally (with probability ( \epsilon )), you choose a machine at random, regardless of the estimated values. This allows you to explore other options that might have been underestimated.
- Let’s say you set ( \epsilon = 0.1 ). This means:
- 90% of the time, you’ll play the machine with the highest estimated value (exploitation).
- 10% of the time, you’ll randomly choose a machine to explore.
- Example:
- Continuing from our earlier estimates ( Q_t(A) = 0.3 ), ( Q_t(B) = 0.4 ), ( Q_t(C) = 0.5 ):
- 90% of the time, you’ll choose Machine C.
- 10% of the time, you’ll pick randomly between Machines A, B, and C.
Step 4: Over Time – Convergence of Estimates
- Law of Large Numbers:
- As you continue to play, the estimated values ( Q_t(a) ) will converge to the true probabilities ( q(a) ). For example, after playing Machine C many times, your estimate ( Q_t(C) ) might get closer to 0.6, which is the true winning probability.
- Balancing Exploration and Exploitation:
- The ( \epsilon )-greedy strategy ensures that you don’t just stick with Machine C based on early estimates—you’ll occasionally try Machines A and B, which might lead to discovering that Machine B is actually the best choice (if, for instance, your initial estimates were off).
Mathematical Implications
- Greedy Method:
- Focuses solely on maximizing immediate reward by choosing the best-known option at each step, which can lead to suboptimal long-term performance if the initial estimates are misleading.
- ( \epsilon )-Greedy Method:
- Provides a mechanism to occasionally explore other actions, improving the chances of finding the globally optimal action in the long run. This balances the short-term gains with the potential long-term discovery of better options.
Summary
- The greedy strategy is like always going with what seems best right now, based on your current knowledge.
- The ( \epsilon )-greedy strategy is like mostly going with what seems best but occasionally trying something new, just in case it turns out to be better.
- Formulas help you keep track of your success and refine your choices. As you gather more data, your estimates ( Q_t(a) ) improve, leading to better decisions over time.
This example should help you see how the math behind these strategies works in a practical, intuitive way, balancing exploration and exploitation to find the best long-term strategy.
Let’s build an intuitive approach to understanding the ( \epsilon )-greedy method with math and formulas. We’ll use a simple, relatable scenario and gradually introduce the mathematical concepts and formulas that guide this approach.
Scenario: Finding the Best Coffee Shop
Imagine you’re in a new town with three coffee shops (A, B, and C). You want to find the coffee shop with the best coffee. However, you don’t know which one is the best, so you need to try each one and learn from your experience.
Step 1: Initial Exploration and Estimation
Trying the Coffee Shops:
- On the first day, you randomly pick one of the coffee shops (let’s say Coffee Shop A) and rate your experience. Suppose you give it a 7 out of 10.
- On the second day, you try Coffee Shop B and rate it a 5.
- On the third day, you try Coffee Shop C and rate it a 9.
Estimating the Quality:
- Initially, you have only one rating per shop:
- ( Q_1(A) = 7 )
- ( Q_1(B) = 5 )
- ( Q_1(C) = 9 )
Here, ( Q_t(a) ) is your estimated quality of coffee shop ( a ) after ( t ) visits.
Step 2: Greedy Selection with Exploration
Now you need a strategy for which coffee shop to visit on the fourth day.
Greedy Strategy:
- If you were using a purely greedy strategy, you would always choose Coffee Shop C because it currently has the highest estimated quality (( Q_1(C) = 9 )).
( \epsilon )-Greedy Strategy:
- The ( \epsilon )-greedy strategy modifies this approach slightly:
- Exploitation: With probability ( 1 – \epsilon ), you choose the coffee shop with the highest estimated quality. In this case, it would be Coffee Shop C.
- Exploration: With probability ( \epsilon ), you pick a coffee shop at random, regardless of the current estimates.
Let’s say you set ( \epsilon = 0.1 ) (meaning 10% of the time you will explore, and 90% of the time you will exploit).
Step 3: Mathematical Formulation
Step-by-Step Calculation:
- Calculate the Estimated Values:
- After each visit, update the estimated value ( Q_t(a) ) for the coffee shop you visited based on the new rating. For example, if you visit Coffee Shop A again and rate it an 8: [
Q_2(A) = \frac{7 + 8}{2} = 7.5
] - In general, if you’ve visited a coffee shop ( a ) ( N_t(a) ) times and received ratings ( R_1, R_2, \dots, R_{N_t(a)} ), the estimated value ( Q_t(a) ) is given by: [
Q_t(a) = \frac{R_1 + R_2 + \dots + R_{N_t(a)}}{N_t(a)}
]- LaTeX:
Q_t(a) = \frac{R_1 + R_2 + \dots + R_{N_t(a)}}{N_t(a)}
- LaTeX:
- Decide Which Coffee Shop to Visit Next:
- Exploit: With probability ( 1 – \epsilon = 0.9 ), choose the coffee shop with the highest ( Q_t(a) ).
- Explore: With probability ( \epsilon = 0.1 ), choose a coffee shop randomly to gather more information.
- Update the Values:
- After each visit, use the new rating to update ( Q_t(a) ) for the visited coffee shop.
Example Calculation:
- Suppose on the fourth day, you follow the ( \epsilon )-greedy approach and:
- With 90% probability, you would go to Coffee Shop C (because ( Q_1(C) = 9 ) is the highest).
- With 10% probability, you randomly choose between A, B, and C.
- If you chose to explore and pick Coffee Shop B at random, and you rate it a 7, then: [
Q_2(B) = \frac{5 + 7}{2} = 6
]
Step 4: Long-Term Behavior and Convergence
- Exploration allows you to potentially discover that Coffee Shop B or A might actually offer better coffee on certain days. Without exploration, you might stick with Coffee Shop C forever, even if it’s not the absolute best in the long run.
- Over time, as you continue to use the ( \epsilon )-greedy strategy, your estimates ( Q_t(a) ) will converge to the true average quality of each coffee shop. The occasional exploration ensures that you don’t miss out on a potentially better option.
Summary of the ( \epsilon )-Greedy Strategy
- Exploitation: Most of the time, you go to the coffee shop that you currently believe is the best.
- Exploration: Occasionally, you try a different shop to make sure you’re not missing out on a better option.
- Math Behind the Strategy:
- The formula ( Q_t(a) = \frac{R_1 + R_2 + \dots + R_{N_t(a)}}{N_t(a)} ) keeps track of the average rating (quality) for each coffee shop.
- The parameter ( \epsilon ) controls the trade-off between exploiting your current knowledge and exploring new possibilities.
By balancing exploration and exploitation using the ( \epsilon )-greedy method, you maximize your chances of finding and consistently enjoying the best coffee in town. This intuitive example, coupled with the mathematical framework, illustrates how the ( \epsilon )-greedy strategy works in practice.
Let’s break down and explain the content in the provided images in detail.
Context: Comparing Greedy and ( \epsilon )-Greedy Methods
The text describes an experiment designed to compare the effectiveness of greedy and ( \epsilon )-greedy methods in the context of the multi-armed bandit problem. Here’s a detailed explanation of the experiment and the results:
Experiment Setup: The 10-Armed Testbed
- Testbed Configuration:
- The experiment involves 2000 randomly generated n-armed bandit tasks where ( n = 10 ). Each of these tasks can be thought of as having 10 slot machines (or “arms”), each with its own unknown probability of payout.
- Action Values: For each bandit, the true action values ( q(a) ) (where ( a = 1, \dots, 10 )) are drawn from a normal distribution with a mean of 0 and variance of 1. This means that the actual value of pulling a particular arm (or selecting a particular action) is uncertain and varies according to this distribution.
- Reward Structure:
- At each time step ( t ), when a particular action ( A_t ) is selected, the reward ( R_t ) is given by the true action value ( q(A_t) ) plus some noise. This noise is also normally distributed with a mean of 0 and variance of 1.
- Averaging Over Bandits: By averaging the performance across these 2000 different tasks (bandits), the experiment can assess the effectiveness of the methods in a statistically meaningful way.
Key Observations: Performance Over Time
The graphs in Figure 2.1 show the performance of the greedy method (( \epsilon = 0 )) and two ( \epsilon )-greedy methods (( \epsilon = 0.01 ) and ( \epsilon = 0.1 )) over 1000 time steps.
- Upper Graph: Average Reward Over Time
- The graph illustrates how the average reward changes as the number of steps increases.
- Greedy Method: Initially, the greedy method (green line) shows a slight improvement in the average reward more quickly than the ( \epsilon )-greedy methods. However, it plateaus at a lower reward level (around 1.0) and doesn’t improve further.
- ( \epsilon = 0.01 ) and ( \epsilon = 0.1 ): These methods continue to improve over time because they keep exploring and updating their estimates of action values. ( \epsilon = 0.1 ) achieves a higher average reward than ( \epsilon = 0.01 ) because it explores more, leading to better identification of the optimal action.
- Lower Graph: Percentage of Optimal Action Selection
- This graph shows the percentage of time the optimal action was selected as the number of steps increased.
- Greedy Method: The greedy method often gets stuck in suboptimal actions. As shown, it correctly identifies and sticks to the optimal action in only about 30-40% of the tasks, and once it commits to a non-optimal action, it doesn’t recover.
- ( \epsilon = 0.1 ) and ( \epsilon = 0.01 ): The ( \epsilon )-greedy methods continue to explore, allowing them to discover and exploit the optimal action more frequently. Over time, the method with ( \epsilon = 0.1 ) selects the optimal action around 90% of the time, while ( \epsilon = 0.01 ) improves more slowly, reaching around 60%.
Analysis: Why ( \epsilon )-Greedy Performs Better
- Greedy Method Limitations:
- The greedy method, by design, stops exploring once it identifies what it thinks is the best action. If this action isn’t actually the optimal one, the method will consistently choose a suboptimal action.
- This leads to a lower long-term average reward and a lower probability of selecting the optimal action.
- Advantages of ( \epsilon )-Greedy:
- Continued Exploration: The ( \epsilon )-greedy methods keep exploring other options, which allows them to correct their course if an early estimate was wrong. This is especially important in complex environments where the best action isn’t immediately obvious.
- Balancing Exploration and Exploitation: By balancing exploration (trying new actions) with exploitation (choosing the best-known action), these methods avoid getting stuck in local optima and improve their chances of finding and sticking to the global optimum.
- Performance Over Time: The results show that as more steps are taken, the ( \epsilon = 0.1 ) method, which explores more aggressively, outperforms the others in both average reward and the probability of selecting the optimal action.
Practical Implications: Choosing ( \epsilon )
- Choosing ( \epsilon ):
- The value of ( \epsilon ) plays a crucial role in the trade-off between exploration and exploitation. A higher ( \epsilon ) means more exploration, which can lead to better long-term performance but might slow down short-term gains. Conversely, a lower ( \epsilon ) leans more towards exploitation, which can yield quicker rewards but might miss out on finding better actions.
- It’s often useful to decay ( \epsilon ) over time, starting with a higher value to encourage exploration and gradually reducing it to focus more on exploitation as the estimates become more accurate.
- Conclusion:
- The experiment shows that ( \epsilon )-greedy methods, particularly with a well-chosen ( \epsilon ), can significantly outperform a purely greedy strategy, especially in environments where the true action values are uncertain and need to be learned through trial and error.
This detailed breakdown provides insight into why ( \epsilon )-greedy strategies are effective, how they compare with greedy strategies, and the importance of balancing exploration and exploitation in reinforcement learning contexts like the multi-armed bandit problem.
The percentage of optimal action is calculated as follows:
- Identify the Optimal Action:
- For each task (or bandit), there is one action that has the highest true action value ( q(a) ). This action is considered the optimal action.
- Track the Selected Actions:
- During the experiment, at each time step ( t ), the algorithm selects an action based on its strategy (e.g., greedy or ( \epsilon )-greedy).
- Check if the Selected Action is Optimal:
- After each action is selected, check whether the chosen action is the optimal action for that specific task. If the selected action matches the optimal action, it is counted as a “correct” or “optimal” selection.
- Count the Optimal Selections:
- Over a given number of steps (e.g., 1000 steps), keep a count of how many times the algorithm selected the optimal action.
- Calculate the Percentage:
- The percentage of optimal action is calculated by dividing the number of times the optimal action was selected by the total number of steps, then multiplying by 100 to get a percentage. For example, if out of 1000 steps, the algorithm selected the optimal action 700 times, the percentage of optimal action would be: [
\text{Percentage of Optimal Action} = \left(\frac{700}{1000}\right) \times 100 = 70\%
]
This percentage gives you an idea of how often the algorithm is choosing the best possible action over time. A higher percentage indicates that the algorithm is effectively identifying and exploiting the optimal action.
This section of the text discusses how the effectiveness of ( \epsilon )-greedy methods compared to greedy methods can vary depending on the nature of the task. Let’s break down the explanation:
1. Impact of Reward Variance
- Higher Reward Variance:
- If the reward variance (how much the rewards fluctuate) is large, say with a variance of 10 instead of 1, the environment becomes “noisier.” In such cases, it takes more exploration to accurately estimate the true value of each action because individual rewards might vary widely from the true average.
- In these noisy environments, ( \epsilon )-greedy methods are likely to perform better relative to greedy methods because they continue to explore and gather more information, which helps in making more accurate estimates of the action values.
- Lower Reward Variance (Zero Variance):
- If the reward variances were zero (meaning the rewards are consistent and predictable), the situation is different. Here, the greedy method might perform best because after trying each action once, you would know the exact value of each action.
- Since there’s no uncertainty, the greedy method can identify the optimal action immediately and stick with it, leading to optimal long-term performance without needing further exploration.
2. Importance of Exploration in Different Scenarios
- Even in Deterministic Environments:
- Even if we assume a deterministic environment (where outcomes are fully predictable after an action is taken), there is still an advantage to exploration if some assumptions are relaxed. For example, if we consider that the true values of actions might change over time (nonstationary environment), exploration becomes crucial.
- In a nonstationary environment, the best action today might not be the best action tomorrow, so the algorithm needs to keep exploring to ensure it adapts to these changes.
- Nonstationarity in Reinforcement Learning:
- Nonstationarity, where the true values of actions change over time, is common in many real-world scenarios and is a significant challenge in reinforcement learning.
- Even if the environment seems stationary and deterministic initially, as learning progresses, the decision-making task may evolve, requiring a balance between exploitation (choosing the best-known action) and continued exploration (trying other actions to check if they’ve become better).
3. Reinforcement Learning and Exploration-Exploitation Trade-Off
- Balancing Exploration and Exploitation:
- Reinforcement learning inherently involves a trade-off between exploration and exploitation. While exploitation can maximize immediate rewards, exploration ensures that the learning algorithm remains flexible and capable of adapting to changes in the environment or discovering better strategies over time.
- The text emphasizes that finding the right balance is crucial, especially in environments where conditions may change, making what was once the best action no longer optimal.
Summary:
- The effectiveness of ( \epsilon )-greedy methods versus greedy methods depends on the nature of the task, particularly the variance in rewards and whether the environment is stationary or nonstationary.
- In environments with high reward variance or nonstationary conditions, exploration (as encouraged by ( \epsilon )-greedy methods) becomes more critical.
- Even in deterministic or stationary environments, exploration can be beneficial if the environment has the potential to change over time, as it ensures that the algorithm doesn’t miss out on better options that may emerge.