Reinforcement Learning: Action-Value Methods wrt Incremental Implementation[Part 6]

Action-Value Method” with respect to Incremental Implementation

The term “Action-Value Method” with respect to Incremental Implementation refers to a strategy used in reinforcement learning to estimate the value of taking a specific action in a given situation (or state) based on the rewards received from past actions. The incremental implementation is a technique used to efficiently update these estimates as new data (rewards) become available, without the need to store all past rewards.

The incremental implementation is a technique used to update the estimated value Q(a)of an action a each time a new reward is received. Instead of recalculating the average reward from scratch (which would require storing all past rewards), the incremental method updates the estimate using the previous estimate and the new reward. This is computationally efficient and requires minimal memory.

1. Context: Estimating Action Values

Action-Value Estimation:
- The goal is to estimate the value 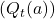$( Q_t(a) )$ of an action 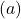$( a )$ based on the rewards received when that action is selected. This is typically done using sample averages of the observed rewards.

2. Basic Approach: Full Memory Implementation

Full Memory Method:
- The most straightforward way to estimate 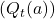is to maintain a complete record of all rewards received after each selection of action 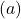. When needed, the estimate 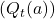can be calculated by averaging all these rewards: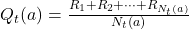
  - This formula sums all the rewards $( R_1, R_2, \dots, R_{N_t(a)} )$ received up to time $( t )$ , then divides by the total number of times $( N_t(a) )$ the action has been selected.
Problem with Full Memory:
- This approach requires storing all past rewards, which means memory and computational requirements grow over time. Every time a new reward is received, the entire sum must be recalculated, which can become inefficient as the number of actions increases.

3. Incremental Implementation: A More Efficient Approach

Incremental Method:
- Instead of storing all the rewards, an incremental update formula can be used. This method requires only the current estimate 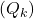$( Q_k )$ and the number of times 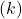$( k )$ the action has been selected so far.
- For some action, if 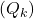is the average reward after ( k-1 ) selections, and 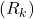is the reward received after the 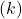-th selection, the updated estimate 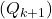can be computed using:
  - Here’s the intuition behind this formula:
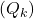  - $( Q_k )$ is your current estimate.
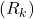  - $( R_k )$ is the new reward.
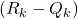  - $( R_k - Q_k )$ represents the difference between the new reward and the current estimate (essentially the “error” in the estimate).
  - The factor 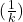$( \frac{1}{k} )$ is the step size, which decreases as more data is collected.
Deriving the Formula:
The formula can be derived as follows:
- Start with the definition of the average: $Q_{k+1} = \frac{1}{k+1} \sum_{i=1}^{k+1} R_i$
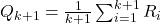
- Break down the sum to separate the new reward $( R_{k+1} ): [Q_{k+1} = \frac{1}{k+1} \left( \sum_{i=1}^{k} R_i + R_{k+1} \right)]$
- Recognize that 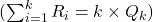$( \sum_{i=1}^{k} R_i = k \times Q_k )$ , which simplifies the expression to: $[Q_{k+1} = \frac{k \times Q_k + R_{k+1}}{k+1}]$
- Rearrange this to reveal the incremental update formula: $[Q_{k+1} = Q_k + \frac{1}{k+1} \left[ R_{k+1} - Q_k \right]]$
Advantages of Incremental Method:
Memory Efficiency: Only the current estimate 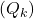$( Q_k )$ and the count 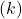$( k )$ need to be stored, not the full history of rewards.
Computational Efficiency: Each update is simple and requires only basic arithmetic operations.

4. General Form of the Update Rule

The incremental update formula can be generalized into a form that occurs frequently in learning algorithms: $[\text{NewEstimate} \leftarrow \text{OldEstimate} + \text{StepSize} \times \left( \text{Target} - \text{OldEstimate} \right)]$
OldEstimate: The previous value of the estimate (e.g., $( Q_k )$ ).
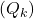Target: The new data point or reward (e.g., $( R_{k+1} )$ ).
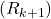StepSize: Controls how much weight is given to the new information; in the case of incremental averaging, it’s $( \frac{1}{k+1} )$
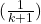
Error Term: The difference between the target and the old estimate 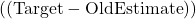$(( \text{Target} - \text{OldEstimate} ))$ is an “error” that the new update tries to correct.

5. Adjustable Step Size

The step-size parameter 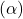$( \alpha )$ in the formula changes from step to step in the incremental method. It’s denoted by 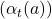$( \alpha_t(a) )$ and sometimes referred to informally as 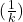$( \frac{1}{k} )$ , where ( k ) is the number of times the action ( a ) has been selected.

Summary

Incremental Implementation is a more memory- and computation-efficient way to update action-value estimates compared to the full memory method.
The incremental update formula allows you to refine your estimate with each new reward, without needing to store all previous rewards or perform complex calculations.
This approach is crucial in environments where computational resources are limited or where actions are selected many times, making it impractical to keep track of every single reward history.

To understand the math behind the incremental implementation intuitively, let’s use a simple analogy and gradually build up to the mathematical concepts.

Scenario: Tracking the Average Score of Your Favorite Team

Imagine you’re a big fan of a sports team, and you’re keeping track of their average score over the season. Every time they play a game, you write down their score. You want to know the team’s average score after each game.

Step 1: Basic Approach – Full Memory Method

Tracking Every Game:

Suppose you’re tracking the team’s score game by game. After 5 games, the scores are 10, 12, 8, 15, and 9.
To calculate the average score after 5 games, you add up all the scores and divide by 5: $[\text{Average after 5 games} = \frac{10 + 12 + 8 + 15 + 9}{5} = 10.8]$

Problem with Full Memory:

This works fine for 5 games, but what if you’re tracking the scores over a whole season with 82 games? Every time you calculate the average, you need to sum up all the scores again and divide by the total number of games.
This approach requires you to remember all the scores, which isn’t a big deal for a few games, but it gets cumbersome as the number of games increases.

Step 2: A Smarter Way – Incremental Update Method

Updating the Average Without Storing All Scores:

Instead of keeping track of every score, you can update the average incrementally as new scores come in.

Intuitive Breakdown:

Current Average:

Let’s say you already know the average score after 4 games is 11.25 (calculated previously).

New Score:

The team just played the 5th game and scored 9 points.

Updating the Average:

Instead of recalculating the average from scratch, you adjust the current average based on the new score.
Here’s the key idea: the new average should be a little closer to the new score than the old average was.
Formula in Plain Words:
$[\text{New Average} = \text{Old Average} + \text{Small Adjustment}]$
The small adjustment is based on how different the new score is from the old average. If the new score is lower than the old average, the new average will decrease slightly; if it’s higher, the new average will increase slightly.

Mathematical Expression:

The adjustment is scaled by how many games you’ve tracked so far. For the 5th game, the adjustment would be scaled by $( \frac{1}{5} )$ :

$[\text{New Average} = \text{Old Average} + \frac{1}{\text{Number of Games So Far}} \times (\text{New Score} - \text{Old Average})]$

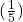Let’s apply this:
Old Average after 4 games $( = 11.25 )$
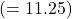
New Score $( = 9 )$
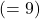
Number of Games So Far $( = 5 )$
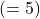
Calculate the adjustment: $[\text{New Average} = 11.25 + \frac{1}{5} \times (9 - 11.25) = 11.25 + \frac{1}{5} \times (-2.25) = 11.25 - 0.45 = 10.8]$
Notice how the new average smoothly adjusts downward from 11.25 to 10.8, reflecting the slightly lower 5th game score without needing to add up all the scores again.

Why This Works: Intuitive Understanding

Small Steps Toward Accuracy:
Each new score is like a small piece of new information. Instead of recalculating everything from scratch, you tweak your current understanding (the old average) just enough to reflect this new information.
Efficiency:
This approach saves you from having to remember every single score. Instead, you just keep track of the current average and the number of games.
Error Correction:
The adjustment term (( \text{New Score} – \text{Old Average} )) acts like an “error correction.” If your old average was off because the new score is higher or lower than expected, this method nudges your average in the right direction.

Summary of the Incremental Update Method

Intuition: Think of it like slowly steering a car toward the center of the lane. Every time you drift a little to one side (the old average), the new score gives you a signal to correct your path slightly.
Efficiency: You don’t need to keep track of every correction (every score), just where you are now (the current average) and how many corrections you’ve made (number of games).
Math: The formula is just a way to automate these small adjustments, making your estimate more accurate with each new piece of information.

This incremental update method is not only intuitive but also practical, especially when dealing with large datasets where recalculating averages from scratch would be inefficient.

When we say that the probabilities of rewards do not change over time, we’re referring to a stationary environment. In a stationary environment, the relationship between actions and their corresponding rewards is fixed and does not vary as time progresses. This means that if you take the same action under the same conditions, the probability of receiving a certain reward remains constant.

Example of a Stationary Environment

Slot Machine (One-Armed Bandit)

Imagine you’re playing a slot machine at a casino. This slot machine has a fixed probability of giving a payout (reward). Let’s say:

The probability of winning (receiving a reward) is 20% every time you pull the lever.
The probability of not winning (no reward) is 80%.

In a stationary environment:

Every time you pull the lever, regardless of how many times you’ve pulled it before or when you pull it, the probability of winning is always 20%.
This does not change over time. Whether it’s your first time playing or your 100th, the chances of winning remain the same.

Key Points in Stationary Environments:

Consistency: The reward distribution for each action stays the same.
Predictability: If you know the reward probabilities, you can predict the expected outcomes of actions without needing to worry that they might change over time.

Example Scenario:

Let’s say you have a simple two-action environment:

Action A: 50% chance of receiving a reward of 10 points.
Action B: 30% chance of receiving a reward of 20 points.

In a stationary environment:

The 50% and 30% probabilities remain the same every time you take Action A or B, no matter how long you play or how often you repeat the actions.

This is in contrast to a nonstationary environment, where these probabilities could change over time (e.g., due to changes in the environment or underlying conditions).

Summary:

In a stationary environment, the relationship between actions and their outcomes is fixed and unchanging. This makes it easier to learn and predict the best actions to take, as the underlying probabilities do not shift over time.