N-Armed Bandit Problem

In the context , the term “bandit” refers to the multi-armed bandit problem in reinforcement learning.

What is a Multi-Armed Bandit?

The multi-armed bandit is a classic problem that serves as a model for decision-making under uncertainty. It is named after slot machines, which are sometimes called “one-armed bandits.” The basic idea is:

• Multiple Actions (Arms): Imagine you’re faced with several slot machines (each with an arm to pull), but you don’t know which one will give you the highest payout.
• Objective: Your goal is to maximize your total reward over time by figuring out which machine (or “arm”) has the highest payout rate.

Why “Bandit”?

The term “bandit” comes from the idea that the machines (or actions) “rob” you of potential rewards if you pick the wrong one. You are trying to “outsmart” the bandits (the different choices) by identifying the best action through trial and error.

Summary

• Bandit here refers to the different choices or actions in a multi-armed bandit problem.
• If the “bandit is changing over time,” it means that the environment is nonstationary, and the rewards for actions can shift, making the problem more complex and requiring different strategies to handle.

• The Learning Problem:
  • You repeatedly choose among 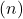different options or actions.
  • After each choice, you receive a numerical reward, which is determined by a stationary probability distribution depending on the action you selected.
  • Your objective is to maximize the expected total reward over time, e.g., across 1000 action selections or time steps.
• The 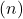-armed Bandit Problem:
  • This problem is named by analogy to a slot machine or “one-armed bandit,” but with 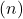levers 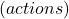instead of one.
  • Each action selection is like pulling one of the slot machine’s levers, with rewards being the payoffs.
  • Through repeated selections, the goal is to maximize winnings by focusing on the best levers.
  • The problem can also be compared to a doctor selecting treatments for patients, where each action has an associated reward (patient survival or well-being).
  • The term “n-armed bandit problem” sometimes refers to generalized versions of this problem, but in this context, it refers specifically to this simple case.
• Action Values in the ( n )-armed Bandit Problem:
  • Each action has an expected or mean reward when selected, referred to as the value of that action.
  • If the value of each action were known, solving the problem would be trivial: simply select the action with the highest value.
  • However, in reality, these values are not known with certainty, though estimates might be available.
• Greedy and Non-greedy Actions:
  • If you select an action whose estimated value is the greatest, it is called a greedy action.
  • Selecting a greedy action is considered exploitation because it relies on current knowledge of action values.
  • If you select one of the non-greedy actions, it is considered exploration because it helps improve the estimate of the non-greedy action’s value.
  • Exploitation aims to maximize the expected reward in the short term, while exploration may lead to better rewards in the long term by discovering better actions.
• The Conflict between Exploration and Exploitation:
  • The dilemma of whether to explore or exploit depends on the precise values of the estimates, uncertainties, and the number of remaining steps.
  • Many sophisticated methods exist to balance exploration and exploitation in mathematical formulations of the -armed bandit and related problems.
  • However, these methods often rely on assumptions about stationarity and prior knowledge, which may not hold in practice.
• Simplified Balancing Methods:
  • Here sophisticated balancing methods are not the focus.
  • Instead, simple balancing methods for the ( n )-armed bandit problem are introduced, which work better than methods that solely exploit.
  • The need to balance exploration and exploitation is a central challenge in reinforcement learning.
  • The simplicity of the ( n )-armed bandit problem helps illustrate this challenge clearly.

This detailed breakdown covers the core concepts and ideas presented in the text, providing clarity on the -armed bandit problem and the exploration-exploitation trade-off.