Self-Attention Mechanism of Transformers [with Easy-to-follow maths and code]

This blog post will get into the mathematical details of the Attention mechanism and create an attention mechanism from scratch using python in an easy to follow , understandable manner.

Before beginning this blog post, I highly recommend visiting my earlier blog post on an overview of transformers. To get the best out of this blog, please check my previous blog post in the following order.

This blog post will get into the nitty-gritty details of the Attention mechanism and create an attention mechanism from scratch using python. The codes and intuitive maths explanation go hand in hand.

What are we going to Learn?

Attention Mechanism concept
Steps involved in Self Attention Mechanism : Step-by-Step Guide with Intuitive Math and Python Implementation

Optimizing Input Pre-Processing: Understanding the Role of Query, Key, and Value Matrix in Attention Mechanism for Natural Language Processing
Exploring Scaled Attention Scores: Essential Concepts in Scaled Attention Scores for Natural Language Processing.

3. Multi-Head Attention Mechanism

So without any further delay, let’s dive in.

via GIPHY

Exploring the Power of Attention Mechanism in NLP and Understanding How Sentences are Processed:-

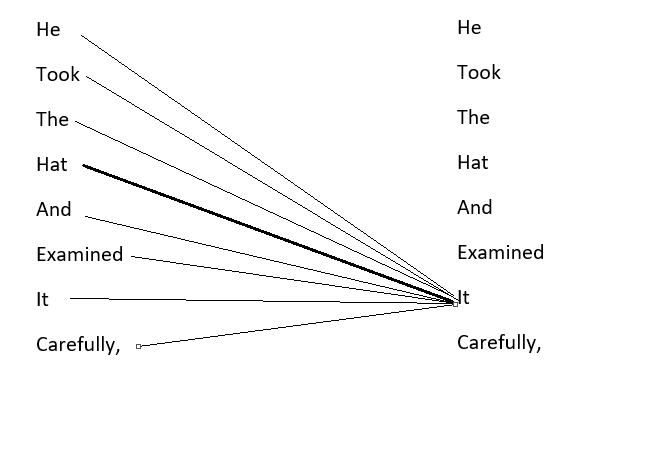
As discussed in the previous post, what happens when a sentence passes through an attention mechanism. When a sentence passes through an attention mechanism, it undergoes a fascinating transformation. Let’s take the example sentence “He took the hat and examined it carefully”. The attention mechanism creates a unique representation, or embedding, for each word, taking into account their relationships with other words in the sentence. In this case, the attention mechanism understands the sentence so deeply that it can associate the word “it” with “hat” and not with “He”. This concept is a crucial aspect of data science, machine learning, and natural language processing, where attention mechanism plays a pivotal role in understanding and processing textual data.

Steps involved in Self Attention Mechanism

1. Cracking the Code of Text Inputs — How Natural Language Processing Transform Words and get it in proper format for Transformers:-

Okay, so here’s the thing: text inputs are not exactly a piece of cake for Transformers or computers to understand. But fear not, we’ve got a clever trick up our sleeves! We represent each word in a text with a vector of numbers, also known as an embedding. Let’s take the sentence “This is book” as an example, and say we’re using an embedding dimension of 5. That means for each word, we’ll have a vector of length 5, like this:

“This”: [0.1, -0.3, 0.5, -0.2, 0.7]

“is”: [-0.6, 0.2, 0.9, -0.1, 0.3]

“book”: [0.8, -0.5, -0.4, 0.6, -0.9]

And voila! We’ve created word embeddings that capture the essence of each word in a numerical form. It’s like giving words their own little numeric superpowers, all in the name of embeddings in natural language processing. Pretty cool, huh?

Input to Transformer

print(f”Shape is :- {np.random.randn(3,5).shape}”)
X=np.random.randn(3,5)
X

Output:-

Alright, folks, buckle up! We’re about to dive into the next level of word embeddings. Remember that input matrix we talked about earlier? Well, from that matrix, we’re going to create some new players on the field: the Key, Query, and Value matrices.

So, here’s the deal: these Key, Query, and Value matrices are like the key ingredients that make the attention mechanism tick. They help the model understand how each word in the input sentence is related to the others.

Just imagine the Key matrix as the secret decoder ring, the Query matrix as the sleuth with a magnifying glass, and the Value matrix as the treasure chest of hidden insights. When combined, they create a powerful trio that unlocks the full potential of word embeddings. Exciting stuff, right? So, stay tuned as we unravel the mysteries of these matrices and discover how they work together to supercharge our text processing game.

2. Obtaining Query, Key and Value matrix

Alright, fellow learners! Now that we know the importance of the Query, Key, and Value matrices, it’s time to dive into the nitty-gritty of obtaining them. But first, let’s have a little fun with some random initiation. Just like rolling the dice in a game, we’ll randomly initialize these matrices for now. But hey, don’t worry, in reality, these are like the superheroes of our neural network, constantly learning and evolving during the training process to become the optimal weights. These are parameters and learned during the training process. The optimal weights are finally used. Assume these weights are optimal weights as shown in the code.

The overall operation involved in this step to be followed in the following code snippets (Image by Author)

Optimized weights for Query Matrix

weight_of_query=np.random.randn(5,3)
weight_of_query

Output:-

Optimized weights for Key Matrix

weight_of_key=np.random.randn(5,3)
weight_of_key

Output:-

Optimized weights for Value Matrix

weight_of_values=np.random.randn(5,3)
weight_of_values

Output:-

These weights will then be multiplied by our input matrix (X) and that will give us our final Key, Query, and value matrix

Calculation of Key Matrix

Key=np.matmul(X,weight_of_key)
Key

Calculation of Query Matrix

Query=np.matmul(X,weight_of_query)
Query

Calculation of Value Matrix

Values=np.matmul(X,weight_of_values)
Values

The first row in the query, key and value matrix denotes query, key, and value vectors of the word “This” and so on for other words. Until now, the query, key, and value matrix might not make much sense. Let’s see how the self-attention mechanism creates a representation(embedding) of each word by finding how each word is related to other words in the sentence by using the query, key, and value vectors.

3. Scaled Attention Scores

The formulae for Scaled attention score:-

dimension=5
Scores=np.matmul(Query,Key.T)/np.sqrt(dimension)
Scores

What happens in Q.K(transpose) is a dot product between query and key matrix and dot product defines similarity as shown in the image below.

Note:- The numbers are all made up in the image below for the sake of explanation and do not add up.

How we calculate attention scores mathematically? (Image by Author)

Hey there! So, we have this cool dot product going on between the query vector q1(This) and all the key vectors k1(This), k2(is), k3(book).
This computation helps us understand how the Query vector q1(This) is related or similar to each vector in the key matrix k1(This), k2(is), k3(book). It’s like a detective work for finding connections!
Now, when we take a closer look at the final output matrix, something interesting pops up. Each word seems to be quite fond of itself, more than any other word in the sentence. It’s like a love affair shown by the diagonal matrix! (i.e. each word is related to itself more than any other words in the sentence as shown by the diagonal matrix as can been seen from the dot product values in the diagonal matrix).
Oh, but there’s also a close bond between “This” and “book”, as highlighted in red in the image above. They seem to be quite the duo!
And hey, check out the last part of the code. We do some fancy normalization by dividing Q.K(transpose) by sqrt(dimension). It’s like a stability trick for the gradients during training. Keeps things smooth and steady, just like a pro!

Softmax in the below code helps to bring it in the range of 0 and 1 and assign probability values.

from scipy.special import softmax
Softmax_attention_scores=np.array([softmax(x) for x in Scores])
Softmax_attention_scores

The above matrix is an intermediate softmax scaled attention score matrix where each row corresponds to the intermediate attention score /probability score for each word in sequence. It shows how each word is related to other words in terms of probability. To get the final attention vector we will multiply the above score with the Value matrix and sum it up. The three attention vectors corresponding to the word “This” is summed up.

In the below code snippet, the softmax_attention_scores[0][0] is the weightage of that particular word, and values[0] is the value vector corresponding to the word “This” and so on.

Softmax_attention_scores[0][0]*Values[0]+\
Softmax_attention_scores[0][1]*Values[1]+\
Softmax_attention_scores[0][2]*Values[2]

Similarly, we can calculate attention for other words like is and book. This is the mechanism of Self-Attention. Next, we will look into the multi-head attention mechanism, which has its underlying principle coming from the Self-Attention Mechanism.

Multi-Head Attention Mechanism Summary:-

The multi-head attention mechanism is a powerful technique used in data science and NLP tasks that involves concatenating multiple self-attention mechanisms together.
Denoting each self-attention process as one head, we can create a multi-head attention mechanism by combining all these heads, allowing for rich contextual information capture.
In our upcoming blog post, during a hands-on exercise, we will observe that each encoder outputs a dimension of 512 with a total of 8 heads.
Each self-attention module generates a (no_of_words_in_sentence, 64) dimension matrix, and when concatenated, the final matrix becomes (no_of_words_in_sentence, (64*8) = 512).
- The last step involves multiplying the concatenated heads with a pre-trained weight matrix, resulting in the output of our multi-head attention mechanism.

In our next blog post, we will discuss about Hugging face implementation of transformers, Until then Goodbye. If you find this helpful, Feel free to check out my other blog posts on transformers:-

via GIPHY